Mystery Planet es un sitio web que ofrece noticias y artículos sobre ciencia y misterios. Para estar al tanto de todo lo que publicamos, además de seguirnos en nuestras redes sociales o suscríbete a nuestro boletín de noticias, te invitamos a nuestro canal de Telegram.
Mucha gente piensa que las matemáticas son una invención humana. Para esta forma de pensar, las matemáticas son como un lenguaje: pueden describir cosas reales en el mundo, pero no «existen» fuera de las mentes de las personas que las usan. Pero la escuela de pensamiento pitagórica de la antigua Grecia tenía un punto de vista diferente. Sus defensores creían que la realidad es fundamentalmente matemática. Más de 2.000 años después, los filósofos y físicos están comenzando a tomar esta idea en serio.

Crédito: Sebastian Mark.
El profesor Sam Baron, de la Universidad Católica Australiana, presenta a continuación algunos argumentos en favor de que la matemática es un componente esencial de la naturaleza que le da estructura al mundo físico.
Abejas y hexágonos
Las abejas en las colmenas producen un panal hexagonal. ¿Por qué?
De acuerdo con la «conjetura del panal» en matemáticas, los hexágonos son la forma más eficiente para embaldosar el plano. Si desea cubrir completamente una superficie utilizando baldosas de forma y tamaño uniformes, manteniendo la longitud total del perímetro al mínimo, los hexágonos son la forma que debe usar.

El patrón hexagonal de panal es la forma más eficaz de cubrir un espacio con baldosas idénticas. Crédito: Ezequiel Junoe.
Charles Darwin razonó que las abejas han evolucionado para usar esta forma porque produce las células más grandes para almacenar miel y la menor entrada de energía para producir cera.
La conjetura del panal se propuso por primera vez en la antigüedad, pero solo fue probada en 1999 por el matemático Thomas Hales.
Cigarras y números primos
He aquí otro ejemplo. Hay dos subespecies de cigarras periódicas norteamericanas que viven la mayor parte de su vida en el suelo. Luego, cada 13 o 17 años (dependiendo de la subespecie), las cigarras emergen en grandes enjambres durante un período de alrededor de dos semanas.
¿Por qué son 13 y 17 años? ¿Por qué no 12 y 14? ¿O 16 y 18?
Una explicación apela al hecho de que 13 y 17 son números primos.

Algunas cigarras han evolucionado para emerger del suelo a intervalos de un número primordial de años, posiblemente para evitar depredadores con ciclos de vida de diferentes longitudes. Crédito: Deb Dowd.
Imagina que las cigarras tienen una variedad de depredadores que también pasan la mayor parte de su vida en el suelo. Las cigarras necesitan salir del suelo cuando sus depredadores están inactivos.
Supongamos que hay depredadores con ciclos de vida de 2, 3, 4, 5, 6, 7, 8 y 9 años. ¿Cuál es la mejor forma de evitarlos a todos?
Bueno, compare un ciclo de vida de 13 años y un ciclo de vida de 12 años. Cuando una cigarra con un ciclo de vida de 12 años sale del suelo, los depredadores de 2, 3 y 4 años también estarán fuera del suelo, porque 2, 3 y 4 se dividen todos equitativamente en 12.
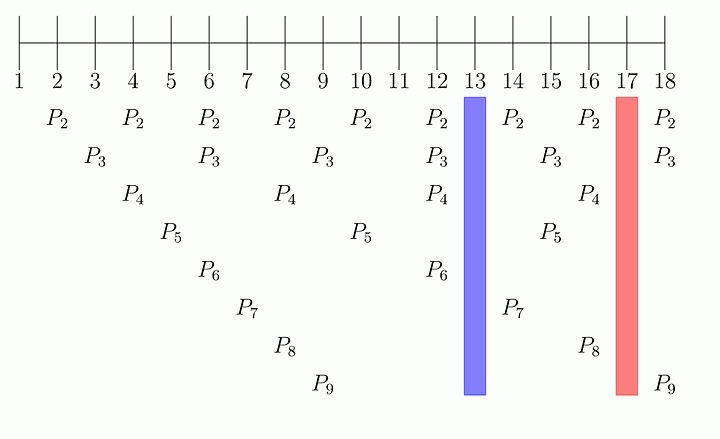
P1 – P9 representan depredadores cíclicos. La recta numérica representa años. Los huecos resaltados muestran cómo las cigarras de 13 y 17 años logran esquivar a sus depredadores. Crédito: Sam Baron.
Cuando una cigarra con un ciclo de vida de 13 años sale del suelo, ninguno de sus depredadores saldrá del suelo, porque ninguno de 2, 3, 4, 5, 6, 7, 8 o 9 se divide uniformemente en 13. Lo mismo ocurre con 17.
Parece que estas cigarras han evolucionado para explotar datos básicos sobre los números.
¿Creación o descubrimiento?
Una vez que empezamos a buscar, es fácil encontrar otros ejemplos. Desde la forma de las películas de jabón hasta el diseño de engranajes en los motores, hasta la ubicación y el tamaño de los huecos en los anillos de Saturno, las matemáticas están en todas partes.
Si las matemáticas explican tantas cosas que vemos a nuestro alrededor, entonces es poco probable que las matemáticas sean algo que hemos creado. La alternativa es que los hechos matemáticos sean descubiertos: no solo por humanos, sino también por insectos, pompas de jabón, motores de combustión y planetas.
¿Qué pensaba Platón?
Pero si estamos descubriendo algo, ¿qué es?
El antiguo filósofo griego Platón tenía una respuesta. Pensaba que las matemáticas describen objetos que realmente existen —e incluían números y formas geométricas—. Hoy en día, podríamos agregar a la lista objetos matemáticos más complicados —como grupos, categorías, funciones, campos y anillos—.
Platón también sostuvo que los objetos matemáticos existen fuera del espacio y el tiempo. Sin embargo, tal punto de vista solo profundiza el misterio de cómo las matemáticas explican algo, pues implica mostrar cómo una cosa en el mundo depende de otra.
Si los objetos matemáticos existen en un reino aparte del mundo en el que vivimos, no parecen capaces de relacionarse con nada físico.
Entra en el pitagorismo
Los antiguos pitagóricos estaban de acuerdo con Platón en que las matemáticas describen un mundo de objetos. Pero, a diferencia de Platón, no creían que los objetos matemáticos existieran más allá del espacio y el tiempo. En cambio, creían que la realidad física está hecha de objetos matemáticos de la misma manera que la materia está hecha de átomos.
Si la realidad está hecha de objetos matemáticos, es fácil ver cómo las matemáticas podrían desempeñar un papel en la explicación del mundo que nos rodea.
En la última década, dos físicos han montado importantes defensas de la posición pitagórica: el cosmólogo sueco-estadounidense Max Tegmark y la física y filósofa australiana Jane McDonnell.
Tegmark sostiene que la realidad es solo un gran objeto matemático. Si eso le parece extraño, piense en la idea de que la realidad es una simulación. Una simulación es un programa de computadora, que es una especie de objeto matemático.
La visión de McDonnell es más radical. Ella piensa que la realidad está hecha de mentes y objetos matemáticos. Las matemáticas son cómo el Universo, que es consciente, llega a conocerse a sí mismo.
Yo defiendo una visión diferente: el mundo tiene dos partes, matemáticas y materia. Las matemáticas dan a la materia su forma y la materia le da a las matemáticas su sustancia.
Los objetos matemáticos proporcionan un marco estructural para el mundo físico.
El futuro de las matemáticas
Tiene sentido que el pitagorismo se esté redescubriendo en la física.
En el siglo pasado, la física se ha vuelto cada vez más matemática, y ha recurrido a campos de investigación aparentemente abstractos, como la teoría de grupos y la geometría diferencial, en un esfuerzo por explicar el mundo físico.
A medida que se difumina el límite entre la física y las matemáticas, se hace más difícil decir qué partes del mundo son físicas y cuáles son matemáticas.
Pero es extraño que los filósofos hayan descuidado el pitagorismo durante tanto tiempo.
Creo que eso está a punto de cambiar. Ha llegado el momento de una revolución pitagórica, una que promete alterar radicalmente nuestra comprensión de la realidad.
¿Te gustó lo que acabas de leer? ¡Compártelo!
Artículos Relacionados





















 Patricio Sepúlveda - 68 cafés
Patricio Sepúlveda - 68 cafés Lucas Daniel A. - 30 cafés
Lucas Daniel A. - 30 cafés Omar S. - 8 cafés
Omar S. - 8 cafés Antonio de Jesús G.V. - 2 cafés
Antonio de Jesús G.V. - 2 cafés
5:34
MATEMATICAMENTE UN ARTICULO PERFECTO Y ....... CON MUCHA SUSTANCIA.! :)